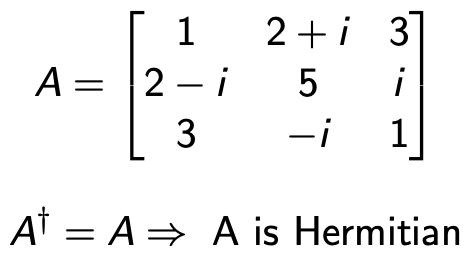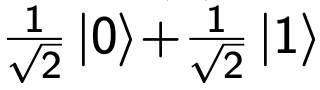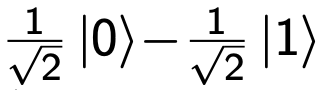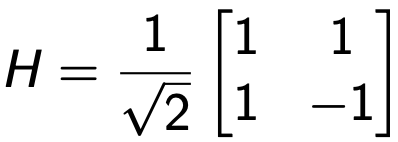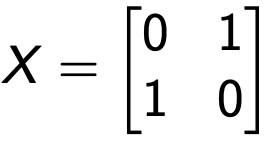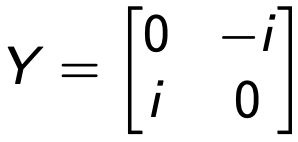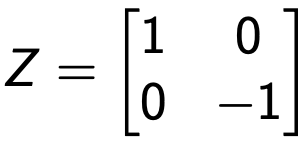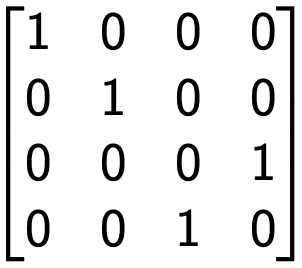È necessario il richiamo di alcune nozioni di Algebra Lineare, molto utili per la progettazione di circuiti quantistici, ricordare il concetto di operatori Hermitiani e Unitari per poter avere accesso all'esame di alcune importanti porte a un qubit (con la loro rappresentazione Qiskit), passando poi a porte a due qubit. Argomenti che sono la spina dorsale per il quantum computing.

TRASPOSTA CONIUGATA A†

La trasposizione coniugata di una matrice complessa A (indicata con A†) è la trasposizione di A (A†) dopo aver preso il coniugato complesso di ogni elemento di A:

Da ricordare che il complesso coniugato di a + bi è semplicemente a - bi (geometricamente, è il riflesso del numero complesso sull'asse reale nel piano complesso).

MATRICE HERMITIANA A = A†

Hermitiano si riferisce a matrici complesse (H ∈ C^2) che sono uguali al loro coniugato complesso: A = A†. Sono matrici i cui autovalori sono sempre numeri reali (λ ∈ R):

OPERATORI UNITARI

Una Trasformazione lineare (T) consente la conversione da uno spazio vettoriale (V) a un altro (W) T: W → V tale che:

• T (v1 + v2) = T (v1) + T (v2): v1, v2 ∈ V
• T (γ × v) = γ × T (v) per ogni scalare γ

Un operatore unitario è un operatore lineare (un operatore che esegue una trasformazione lineare), con l'ulteriore vincolo che è unitario: AA† = A†A = I.

I rappresenta la matrice Identità, detta anche matrice identica o matrice unità, è una matrice diagonale in cui gli elementi della diagonale principale sono tutti 1. In modo equivalente, possiamo definire la matrice identità come una matrice quadrata che ha tutti 1 sulla diagonale principale e tutti 0 altrove.

Ciò significa é possibile applicare un operatore unitario a uno spazio vettoriale, applicare il suo inverso e ottenere lo spazio vettoriale originale. Son fondamentali perché questo è esattamente il modo in cui operano le porte quantistiche: con una proprietà di reversibilità.

GATE QUANTISTICI

Una porta quantistica è un'analogia delle porte classiche ed è anche un paradigma utile per pensare alla manipolazione dei qubit.

Conosciute anche come porte logiche quantistiche, hanno le seguenti proprietà:

• Reversibile, a differenza di alcune porte classiche (ad esempio la porta OR)
• Rappresentate da matrici Unitarie
• Ogni gate viene applicato solo allo stesso numero di qubit (porte a un qubit, porte a due qubit,...)

HADAMARD GATE

Il gate Hadamard viene applicato a un singolo qubit.

Se il qubit è in uno stato | 0⟩, dopo l'Hadamard, sarà in una sovrapposizione di:

Se si trova in | 1⟩ finirà in:

È essenziale creare una sovrapposizione da | 0⟩. Si può verificare utilizzando la versione vettoriale del qubit e il seguente operatore unitario:

Si può inoltre verificare che HH† = H†H = I.

In Qiskit si può creare e testare il circuito quantistico:

X GATE (PAULI-X)

Il gate X (noto anche come Pauli-X) viene applicato a un singolo qubit.

Può essere visto come l'equivalente della porta NOT nei circuiti classici, rispetto alla base zero-uno. Mappa lo stato | 0⟩ in | 1⟩ e lo stato | 1⟩ in | 0⟩. Si dice che effettua un cambio di bit (bit-flip).

Si può verificare utilizzando la versione vettoriale del qubit e il seguente operatore unitario:

Si può inoltre verificare che XX† = X†X = I.

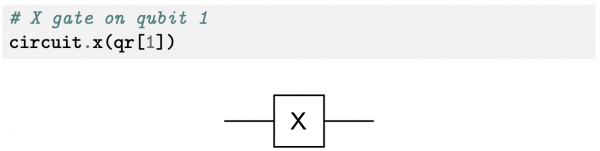
In Qiskit si può creare e testare il circuito quantistico:

Y GATE (PAULI-Y)

Il gate Y (noto anche come Pauli-Y) viene applicato a un singolo qubit.

Di solito è chiamato inversione di fase perché mappa | 0⟩ in i | 1⟩ e | 1⟩ in −i | 0⟩.

Si può verificare utilizzando la versione vettoriale del qubit e il seguente operatore unitario:

Si può inoltre verificare che YY† = Y†Y = I.

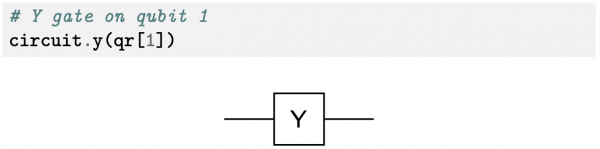
In Qiskit si può creare e testare il circuito quantistico:

Z GATE (PAULI-Z)

Il gate Z (noto anche come Pauli-Z) viene applicato a un singolo qubit.

Di solito è chiamato inversione di fase (phase-flip) perché lascia lo stato | 0⟩ invariato e mappa | 1⟩ su - | 1⟩.

Si può verificare utilizzando la versione vettoriale del qubit e il seguente operatore unitario:

Si può inoltre verificare che ZZ† = Z†Z = I.

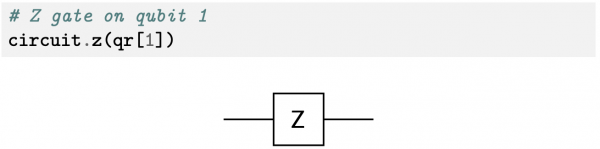
In Qiskit si può creare e testare il circuito quantistico:

Una curiosità: Il quadrato delle matrici delle porte di Pauli (X, Y, Z) sono l'identità stessa: X^2 = Y^2 = Z^2 = I.

CONTROLLED GATES

I controlled gates sono un'estensione dei gate di ordine inferiore. Di solito, eseguono la stessa operazione, ma utilizzano uno o più qubit aggiuntivi che vengono utilizzati per controllare/accertare se l'operazione originale deve essere applicata.

Ad esempio, i controlled gates per 2 qubit aggiungono un qubit di controllo e:

• se è | 1⟩, il gate originale viene applicato all'altro qubit
• se il qubit di controllo è | 0⟩ l'altro qubit rimane lo stesso (tipicamente).

Dati due qubit, capovolge il secondo se e solo se il primo è | 1⟩.

CNOT - CONTROLLED NOT (CX)

Un esempio di Controlled Gate è il gate CNOT, uno dei più importanti gate a 2 qubit. È un gate controllato derivato dal gate X, quindi è anche noto come gate CX. Il suo operatore unitario è:

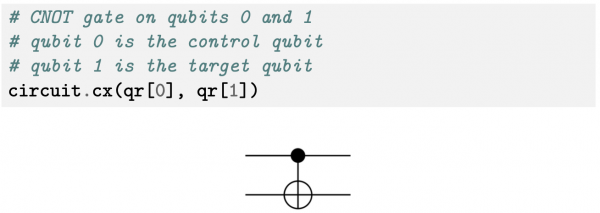
In Qiskit si può creare e testare il circuito quantistico:

ALTRI GATES

Man mano che ci si immerge più in profondità nel Mondo Quantistico, si presenteranno più porte.

E’ importante sapere che è possibile inoltre anche crearne di proprie (da ricordare principalmente le loro proprietà e va controllato se nessuno le ha ancora inventate). Di seguito alcuni altri nomi di porte quantistiche che si incontreranno:

• SWAP
• Phase shift family
• CCNOT (detta anche TOFFOLI Gate)
• CSWAP (C stà per CONTROLLED)
• XX
• Deutsch