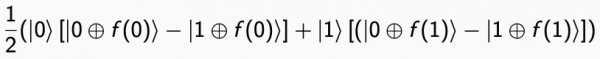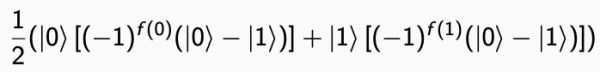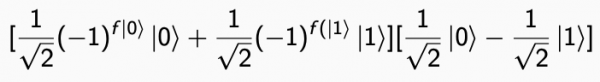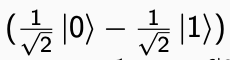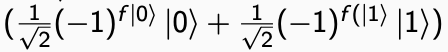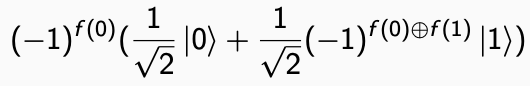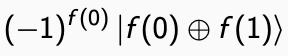Si può mostrare efficacemente come un computer quantistico potrebbe battere uno classico esplorando l'algoritmo di Deutsch (e il suo caso generale Deutsch-Jozsa). Non risolve un problema particolarmente interessante nell'informatica classica, ma evidenzia il potere quantistico.

ORACOLI QUANTISTICI

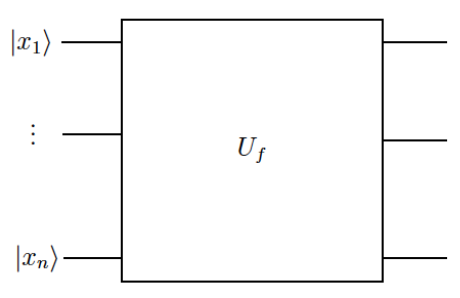
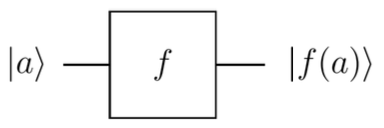
Gli oracoli quantistici sono un'utile astrazione per scrivere algoritmi quantistici. Un oracolo nasconde una funzione che accetta un numero di qubit come input, esegue una trasformazione e produce lo stesso numero di qubit come output. Può essere visto come scatola nera (reversibile):

Alcuni motivi per utilizzare gli oracoli sono:

•     Semplificazione concettuale dei circuiti

•     Consentire il confronto tra algoritmi classici e quantistici

•     Facilitare l'interpretazione visiva dei circuiti quantistici

Questo approccio è abbastanza utilizzato nella specifica di nuovi algoritmi quantistici, in quanto consente di astrarsi dal non necessario, seguendo le linee del "Principio di astrazione" dell'informatica.

CALCOLO QUANTISTICO REVERSIBILE

Si desidera che i calcoli quantistici siano reversibili: questa è una conseguenza voluta della natura unitaria delle porte quantistiche. Tuttavia, si deve anche essere in grado di estrapolare questa nozione di reversibilità agli oracoli, in modo da essere certi (attraverso una sorta di induzione implicita) di non perdere la proprietà di reversibilità indipendentemente dalla complessità del circuito.

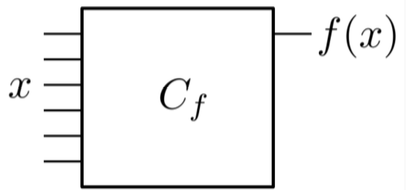
Se si considera un circuito classico per calcolare un operatore booleano:

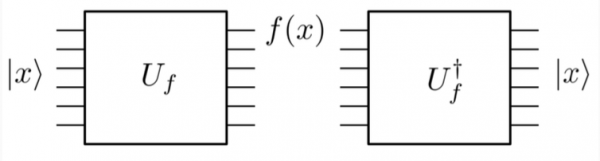
Se lo si facesse nei circuiti quantistici, si perderebbero tutte le informazioni su “x” e, quindi, verrebbe distrutta ogni possibilità di reversibilità. Quello che si vuole veramente è un modo in cui si possa applicare il gate inverso di Uf, Uf †:

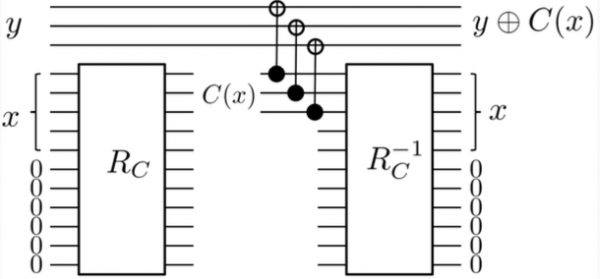
Raggiungere questo obiettivo è più facile di quanto sembri poiché si posseggono già gli strumenti. Si è già in grado di calcolare qualsiasi funzione e poi riportarla allo stato originale, poiché si utilizzano solo operatori unitari. Ma farlo significa tornare all'inizio. Tuttavia, se si usano alcuni "helper qubit", ci si potrebbe trovare in qualcosa di simile:

Infatti l'equivalente della porta CNOT nelle porte logiche è l'OR esclusivo (XOR) e può essere utilizzato per copiare il risultato di C (x) sui qubit y, se ciascuno di quei qubit in y = | 0⟩ (0 XOR A = A):

Ciò significa che è possibile ottenere la nozione di reversibilità induttiva se si applicano le operazioni che si desiderano sui qubit di input, salvandole usando tante porte CNOT quante sono il numero di qubit nel risultato e ripristinando i qubit ottenuti applicando le operazioni inverse per ritornare all'ingresso originale. La differenza è che si possiede anche il risultato.

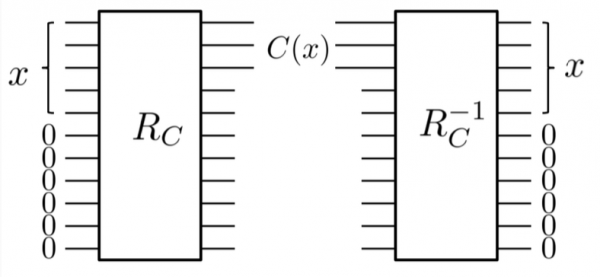
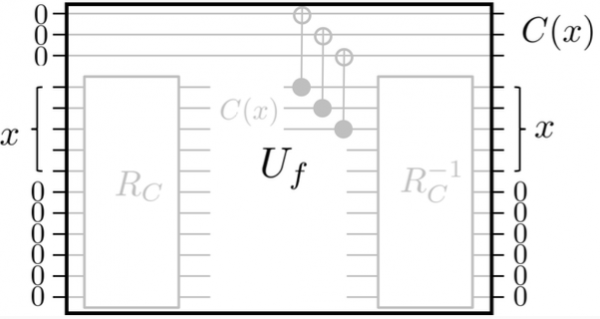
Alla fine, anche se si necessita di qubit extra azzerati, è possibile astrarre il circuito su una mappatura reversibile, poiché non si perdono mai, ma solo si guadagnano, informazioni:

FORMULAZIONE DEL PROBLEMA DEUTSH-JOZSA

Si consideri una funzione f: {0, 1} n → {0, 1} che mappa un array di n bit in 0 o 1. Non è nota la logica sottostante. Si sa che è costante o bilanciata:

•     Costante: il suo output è sempre 0 o sempre 1

•     Bilanciata: emette 0 per metà del valore di ingresso e 1 per l'altra metà

Nel caso n = 1 si ha f: {0,1} → {0,1} che mappa un singolo bit in 0 o 1. Se è fornita una scatola nera, un oracolo, che prende come input questi due bit e restituisce il valore sconosciuto:

Per rispondere a questa domanda in modo classico, si avrebbe sempre bisogno di due invocazioni di funzioni. Si potrebbe eseguire f (0) e f (1) e vedere se è costante o bilanciata.

ALGORITMO CLASSICO

Un'alternativa è controllare cosa produrrebbe il valore di f (0) XOR f (1):

•     f (0) XOR f (1) = 0 → costante

•     f (0) XOR f (1) = 1 → bilanciata

Tuttavia, ciò richiederebbe ancora due invocazioni della scatola nera.

ALGORITMO QUANTISTICO

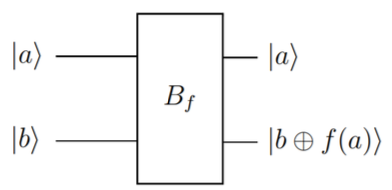
Prima di trasformarlo in un problema quantistico, si necessita che la scatola nera sia un oracolo che consente il calcolo reversibile, in questo modo:

ALGORITMO DI DEUTSCH

Si immagini la seguente procedura:

•     Si inizia con due qubit, q0 nello stato | 0⟩ e q1 nello stato | 1⟩ (| 01⟩).

•     Si applica un Hadamard a ogni qubit

•     Il risultato è ½ (| 00⟩ - | 01⟩ + | 10⟩ - | 11⟩)

•     Si invoca l’oracolo, che mappa | ab⟩ o | a⟩ | b⟩ in | a⟩ | b ⊕ f (a)⟩

•     Il risultato è: ½ (| 0⟩ | 0⊕f (0) ⟩− | 0⟩ | 1⊕f (0)⟩ + | 1⟩ | 0⊕f (1) ⟩− | 1⟩ | 1⊕f (1)⟩)

Semplificando:

 Si può usare la seguente equivalenza:

Per sostituire sopra e ottenere:

Separandolo nella forma a 2 qubit:

Il secondo qubit può essere ignorato:

ciò che rimane è il primo qubit:

che contiene sia f (0) che f (1). Entrambe le immagini di f con un solo passaggio sull'oracolo. Questo può essere ulteriormente semplificato in:

Infine, applicando un gate Hadamard sul qubit (si può provare a farlo su carta) si arriva a:

Il significato è il seguente:

•     se f è costante (00 o 11) → l'uscita è 0 (XOR è 0)

•     se f è bilanciata (01 o 10) → l'uscita è ± 1 (XOR è 1)

ovvero che è possibile fare un singolo passaggio sul gate dell'oracolo per scoprire se è costante o equilibrata: un'impresa impossibile nell'informatica classica.

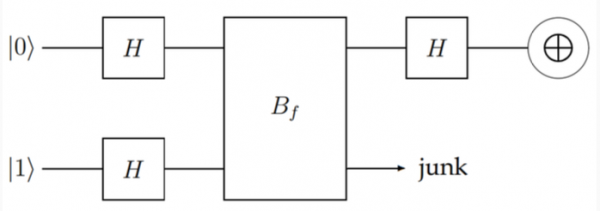
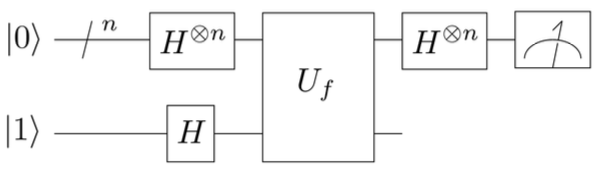
In estrema sintesi, ciò che è stato fatto è seguire il seguente circuito:

Come si nota, è uno dei circuiti quantistici più semplici da progettare ma, tuttavia, ingenera qualche difficoltà nel capire come e perché ha funzionato. Gli algoritmi quantistici sono generalmente difficili all'inizio poiché richiedono un nuovo modo di affrontare i problemi.

ALGORITMO DI DEUTSCH-JOZSA

Tornando alla funzione f: {0,1} n → {0,1} dovrebbe essere noto che la soluzione all'istanza n = 1 è generalizzata per rispondere alla stessa domanda su un array n-dimensionale con un solo passaggio sulla scatola nera (un algoritmo classico richiederebbe 2n − 1 + 1 passaggi).

Usando n qubit inizializzati a 0 e 1 a 1, eseguendo le stesse operazioni, ma su più qubit:

Nota: Qiskit non consente gli oracoli poiché richiederebbe un approccio piuttosto impegnativo (dovrebbe essere in grado di interagire con l'hardware reale), ma si possono semplicemente scegliere un paio di operazioni invece di una scatola nera e implementare l’algoritmo di Deutsch attorno a queste.