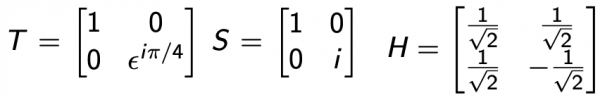Gli argomenti contenuti in questo articolo sono di solito tipicamente accennati o trattati in precedenza quando si apprende il quantum computing, ma potrebbe essere più facile comprenderli dopo la lettura dei precedenti. Ad ogni modo, alcuni di questi, sono anche prerequisiti per il contenuto successivo.

Si inizia con alcune considerazioni in più sui circuiti quantistici (vale a dire porte universali), un esempio delle conseguenze degli operatori unitari per approdare infine all'entanglement con note introduttive sulla notazione Big O.

PORTE UNIVERSALI CLASSICHE

Nel Calcolo Classico, qualsiasi calcolo è realizzabile tramite alcuni semplici insiemi di porte: ad esempio l'insieme {AND, NOT} permette di derivare qualsiasi altro operatore. Inoltre, ci sono insiemi singoli che lo consentono, come l'insieme {NAND} (si può come esempio provare a simulare un OR usando solo NAND).

PORTE UNIVERSALI QUANTISTICHE

Dopo che si pensò inizialmente al Quantum Computing (in realtà il calcolo reversibile è arrivato prima), con lo sviluppo di porte quantistiche furono concepiti anche questi semplici insiemi, che esistono sebbene richiedano alcune considerazioni più complesse e troppo teoriche. Ad ogni modo é possibile dare uno sguardo a quelle di cui si ha bisogno.

In primo luogo, non è possibile farlo utilizzando solo operatori a qubit singoli (alcuni li conosciamo già, altri sono qui riportati a scopo di completezza).

Dato ε^ix = cos(x) + i sin(x):

Il primo modo per ottenere l’insieme delle Universal Gate è prendere questi gate a qubit singoli e includere il gate CNOT.

La Toffoli gate (CCNOT) è una delle più eloquenti porte che possono eseguire qualsiasi operazione booleana (universale per il calcolo reversibile booleano). Tuttavia, da solo non è sufficiente per l'universalità quantistica. Ma se, attraverso il gate Hadamard, si aggiunge la capacità di generare la sovrapposizione, formano un insieme di dimensione due che è capace di calcolo quantistico universale {Toffoli, H}.

La trasformazione della porta Toffoli mappa 3 qubit ed è quindi di dimensione 2^3 = 8. È essenzialmente una matrice identità, fatta eccezione per l'intersezione delle ultime due colonne e due righe, che corrisponde al gate X:

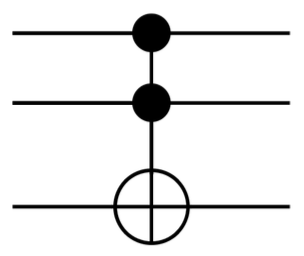
Il Toffoli gate è rappresentato dal seguente simbolo; si nota qualche somiglianza con il cancello CNOT visto che è anche chiamato CCNOT. I cerchi neri rappresentano infatti entrambi i bit di controllo:

PORTE E BASI

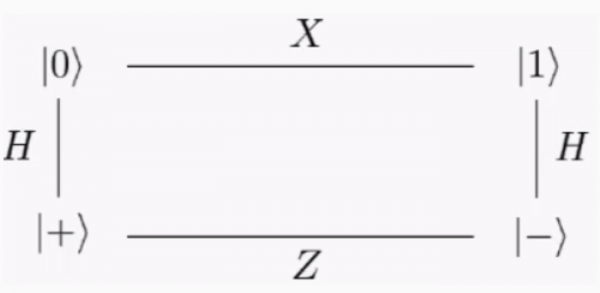
Il diagramma sotto è un'utile scorciatoia per la conversione degli stati quantistici utilizzando porte quantistiche e descrive anche le conseguenze del calcolo reversibile. Letteralmente, si può avere un qubit in uno qualsiasi dei quattro stati | 0⟩, | 1⟩, | −⟩, | +⟩ e ottenerne qualsiasi altro eseguendo semplici porte di un qubit:

Si può provare partendo con lo stato sotto (vettore di stato 0) per ottenere ciascuno degli altri stati, concatenando le rispettive operazioni all’interno del digramma ciclico:

ENTANGLEMENT

L'entanglement è un fenomeno curioso a livello quantistico. Descrive lo stato di un sistema in cui lo stato quantistico di due o più particelle non può essere considerato indipendentemente l'una dall'altra. Esiste una correlazione tra le loro proprietà quantistiche.

Pragmaticamente, se due qubit sono intrecciati, misurarne uno produrrà la misura sull'altro come costante, quando l'esperimento viene ripetuto molte volte, essi risultano intrecciati.

Questa proprietà è valida su lunghe distanze nonostante l'incertezza sulla domanda a cui si inizia ad essere abituati.

POSSIBILITA' DELL'ENTANGLEMENT

Questa proprietà comporta l’essere tanto potenziale quanto controversia: perfino Albert Einstein ne ha contestato la possibilità. La sua esistenza è, tuttavia, indiscutibile (senza entrare nelle opinioni paradossali o discutere sulle diverse interpretazioni per esso).

Se ne fa molto uso (come ad esempio il gate CNOT): lo stato di un qubit controlla il capovolgimento dell'altro.

Nel calcolo classico ciò significherebbe che sono dipendenti, ma in termini quantistici sono entangled, non solo dipendenti, perché se si applica questa porta ai qubit in sovrapposizione, otteniamo un risultato non deterministico che è correlato deterministicamente.

NOTAZIONE BIG O

La notazione Big O viene utilizzata per descrivere il comportamento limitante di un algoritmo (scenari del caso peggiore), fornendo essenzialmente una stima della complessità (che riflette come il tempo di esecuzione evolve con la dimensione dell'input).

La notazione è O (COMPLEXITY).

• Si suppone di avere un ciclo classico su un array di dimensione N. La complessità di questo algoritmo nella notazione Big O, sarebbe O (N).
• Se si dovessero calcolare i valori quadrati di ogni cella in una matrice N × N, la sua complessità sarebbe O (N^2)
• Una tipica “ricerca binaria” ha una complessità di O (log-base-2 (N))

I problemi computazionali sono descritti dall'algoritmo più efficiente in grado di risolverli.

I problemi P (polinomiali) sono classificati come facili/risolvibili/trattabili in modo efficiente, per via della quantità di tempo necessaria per risolvere istanze sempre più grandi in cui evolve in modo polinomiale.

I problemi NP (tempo polinomiale non deterministico), invece, non sono considerati risolvibili in modo efficiente. Ciò significa che all'aumento lineare delle dimensioni delle istanze del problema, il tempo (a volte lo spazio) richiesto cresce esponenzialmente. Non deterministico implica non risolvibile su una macchina di Turing deterministica.

NOTAZIONE BIG O - IMPATTO QUANTISTICO - BQP

Quando si entra nel Mondo Quantistico emerge una nuova classe di problemi: il tempo polinomiale quantistico a errore limitato BQP, una classe di problemi risolvibili in tempo polinomiale in un computer quantistico (con una probabilità di errore ≤ 1/3)

NOTAZIONE BIG O - IMPATTO QUANTISTICO - NP VS BQP

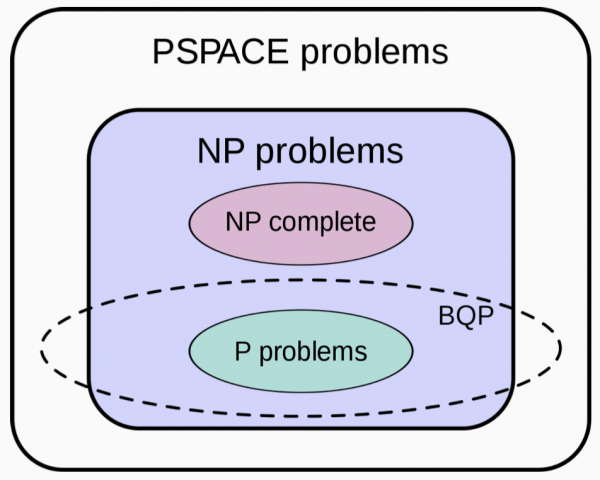
Il problema con questa classe è che riflette la potenza del calcolo quantistico, poiché alcuni problemi classici che appartengono alla classe NP possono essere risolti in BQP.

Ciò che non è chiaro è fino a che punto possono spingersi i computer quantistici: BQP è un sottoinsieme di NP o viceversa? Corrispondono? Rispondere a queste domande darebbe un'impronta definitiva alla potenza del Quantum Computing rispetto al Classical Computing.