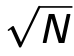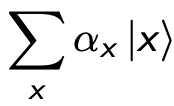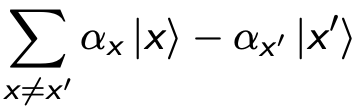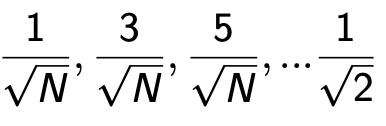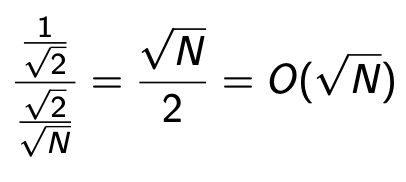Esiste un algoritmo quantistico, famoso e pragmatico, per eseguire una ricerca: l'algoritmo di Grover.

È interessante da analizzare da un punto di vista astratto, ovvero nella comprensione dell'amplificazione di ampiezza: inversione di fase + inversione della media, per capirne lo scopo e come si confronta con le strategie di ricerca classiche che risolvono gli stessi problemi

IL PROBLEMA DELLA RICERCA

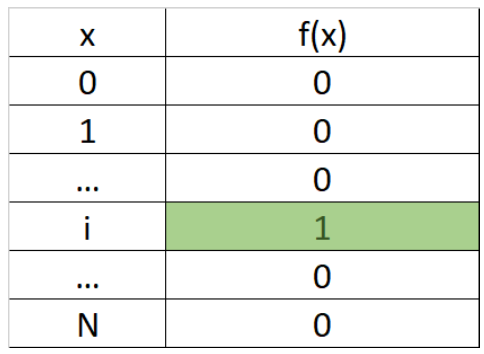
Si suppone di avere una funzione f: {0,1, ..., N − 1} → {0,1} per la quale si desidera trovare i valori di x per cui f (x) = 1. Per semplificare e anche per rendere il problema più difficile, si suppone che esiste una sola x di questo tipo:

Un programmatore classico affronterebbe il problema in questo modo:

•     Ricerca sequenziale tramite x ∈ [0, N] fino a f (x) = 1

•     Ricerca casuale con x ∈ [0, N] fino a f (x) = 1

•     ...

Tutto abbastanza semplice e nello scenario peggiore genera N ricerche e media N/2.

PROBLEMA SAT

Oltre ai problemi più ovvi, si dovrebbe anche conoscere il problema SAT (problema di soddisfacibilità booleano) che riguarda la determinazione dei valori per le variabili booleane in modo che l'espressione booleana associata restituisca true.

Questo è un problema computazionalmente costoso e rientra nella categoria NP (in verità NP-complete). Molti problemi, come la pianificazione, possono essere convertiti in una formulazione SAT, utilizzando i solutori SAT esistenti per trovare facilmente soluzioni per nuovi problemi.

SAT, in quanto tale, può essere visto come un problema di ricerca, in cui è necessario trovare la combinazione precisa di valori booleani che restituisce true.

ALGORITMO DI GROVER

Il dottor Lov Grover ha ideato un algoritmo che, invece di N passaggi per trovare una soluzione, richiede un numero di passaggi pari a:

Questo è l’ottimale ed è impossibile velocizzare ulteriormente. L'algoritmo fa uso di due fenomeni molto importanti di inversione che possono essere implementati in un computer quantistico:

• Inversione di fase

• Inversione sulla media (media)

• Un oracolo per la funzione f

INVERSIONE DI FASE

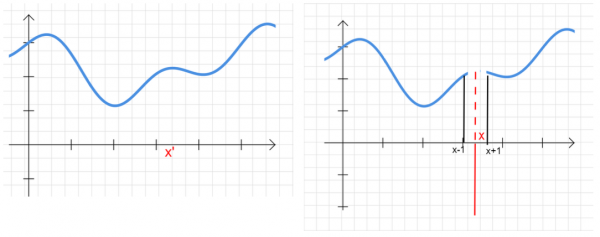
Il fenomeno dell'inversione di fase aiuterà a trovare x′ in modo che f (x′) = 1. Si immagini una sovrapposizione quantistica su tutti i possibili valori x:

alla quale è possible, attraverso l'uso dell’oracolo, ottenere:

Ciò significa che, tracciando αx per ogni valore x, si otterrà qualcosa di simile al seguente diagramma (astratto) - in cui il valore corretto è stato invertito (anche se non ne conosciamo il valore):

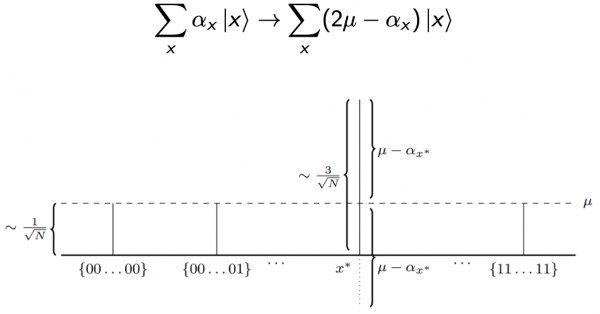
INVERSIONE SULLA MEDIA

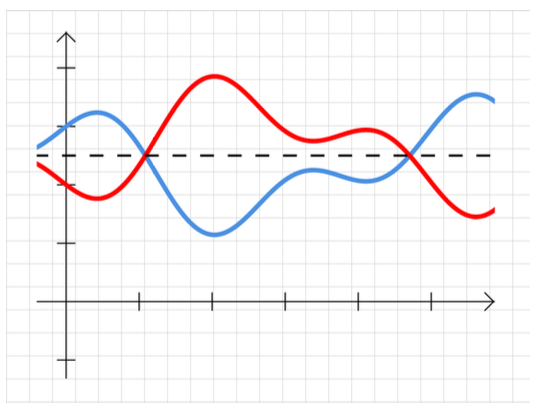
La fase successiva dell'algoritmo consiste nel prendere quella stessa distribuzione di peso e rispecchiarla sull'altro lato della media: questo può essere fatto in un circuito quantistico. Quanto segue è una rappresentazione di questa trasformazione (entrambe le funzioni sono l'inversione rispetto alla media dell'altra):

Lo si fa per il seguente motivo: si considerino i due passaggi appena effettuati: inversione di fase e quindi inversione sulla media. La prima, imposta la soluzione per essere un pò più riconoscibile, la seconda operazione separa ulteriormente il risultato dal resto degli stati possibili. Se si reiterano questi due passaggi, si separerà ulteriormente la risposta corretta dalle altre. Il numero di volte da eseguirli per ottenere un'alta probabilità garantita di avere la risposta giusta è √N.

ALGORITMO DI GROVER (PERCHÈ √ N)

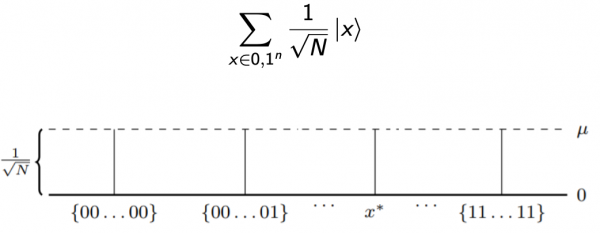
Si suppone di inizializzare n qubit a | 0⟩, ogni qubit può essere paragonato a un valore booleano sulla soluzione di n bit che stiamo cercando. Si crea quindi una sovrapposizione che li pone in una sovrapposizione uniforme (ogni stato ha uguale probabilità):

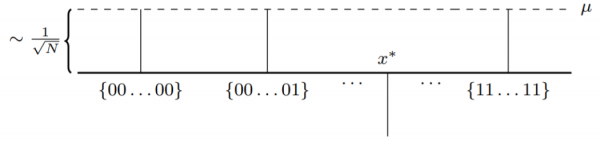
Quindi si crea un oracolo quantistico Of che capovolgerà i qubit se il risultato è 1 e si applica questo gate, ciò  applica effettivamente un'inversione di fase:

Infine, si applica l'inversione sulla media:

Ripetendo il meccanismo, si nota che l'ampiezza migliora (per passo) √ 2 / √N ad ogni iterazione:

Al punto di 1/√2 si ha un'alta probabilità di misurazione garantita, risultante nella soluzione. Questo quanto ci si impiegherà per arrivarci:

AMPLIFICAZIONE DI AMPIEZZA

Questa combinazione di inversione di fase e inversione della media è chiamata Amplificazione di ampiezza.

Si nota che l'ampiezza non può aumentare per sempre e alla fine sarà così grande che la media diventa negativa (dopo l'inversione di fase) e l'inversione del gradino medio danneggia il risultato. È quindi importante sapere quando fermarsi (quante iterazioni garantiscono l'ampiezza minima desiderata).

Ecco fatto. Eseguendo l'iterazione di Amplificazione di ampiezza è possibile risolvere un problema classico che aveva una complessità di O (N) in O (√N): non è una crescita esponenziale (come sono in grado di fare alcuni algoritmi quantistici), ma ciò comporterebbe delle conseguenze davvero dirompenti.