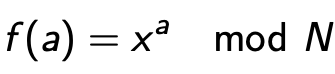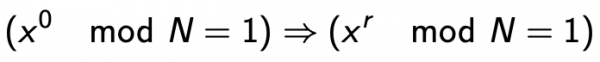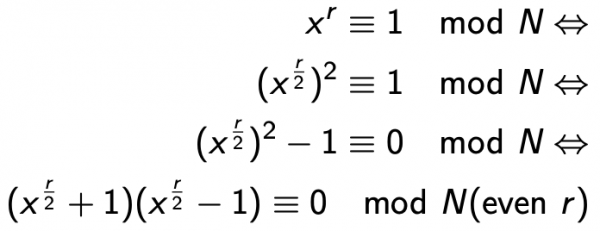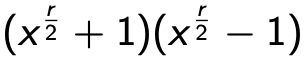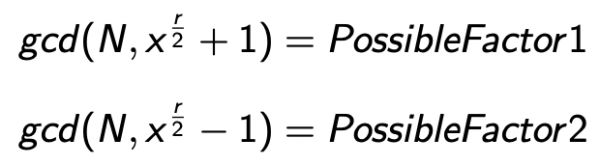È l'algoritmo quantistico che, probabilmente, ha avuto l'impatto più sorprendente sul mondo e ha contribuito ad aumentare l'interesse per il Quantum Computing e a raggiungere l’odierna massa critica.

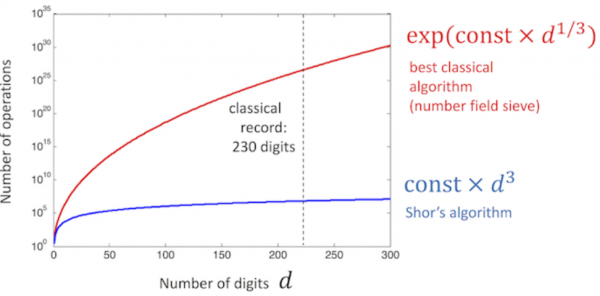
A differenza di altri algoritmi quantistici, questo prende il nome dal suo creatore: Peter Shor (algoritmo di Shor). Porta un'accelerazione esponenziale su un problema molto importante al giorno d'oggi: la scomposizione in fattori primi.

IL PROBLEMA DELLA FATTORIZZAZIONE

Dato un numero N si desidera trovare una coppia di numeri primi (p, q) il cui prodotto è uguale a N: p × q = N. L'esistenza di questa coppia è garantita dal teorema fondamentale dell'aritmetica.

Esistono già algoritmi per raggiungere questo obiettivo, tuttavia questo problema rientra nella famiglia NP ed è computazionalmente possibile solo per piccoli valori di N, dal momento che i computer classici non sono in grado di trovarlo in un tempo accettabile.

CONSIDERAZIONI SULLA CRITTOGRAFIA

Il processo opposto di trovare grandi numeri primi è relativamente facile - test di Primalità o Setaccio di Eratostene - così come lo è moltiplicarli (Test di primalità, Crivello di Eratostene).

In quanto tali, molti algoritmi di crittografia si basano su tale facilità e sulla “durezza” della fattorizzazione per fornire un mezzo di comunicazione sicuro. Se questo sembra ancora strano, diciamo solo che l'affidabilità della maggior parte delle richieste effettuate dal un browser ai server online si basa su di esso, per non parlare degli altri innumerevoli meccanismi di crittografia disponibili 

PANORAMICA DELL’ALGORITMO DI SHOR

Costituirebbe un vero problema se la scomposizione in fattori primi diventasse un problema risolvibile: il mondo dovrebbe essere ridefinito da zero e si verificherebbero innumerevoli conseguenze sulla privacy e sulla sicurezza dei dati, di proporzioni inimmaginabili. È un dato di fatto. Questo è ciò che Peter Shor ha concepito (e il suo nome appartiene sicuramente all'algoritmo).

L'unico ostacolo che impedisce questo evento catastrofico è che i veri computer quantistici sono ancora a pochi passi dal consentire calcoli così complessi. Si potrebbe affermare che per fortuna si è scoperta la teoria prima che arrivasse la tecnologia.

Dal punto di vista tecnico, l'algoritmo di Shor risolve la scomposizione in fattori primi attraverso i seguenti passaggi:

1.   Formulazione della scomposizione in fattori primi come problema di individuazione del periodo

2.   Algoritmo quantistico per risolvere la ricerca del periodo

3.   Conversione del periodo in fattori primi

Aldilà di esaminare ciascuno di questi, il cuore dell'accelerazione risiede nell'algoritmo quantistico in questione: la trasformata quantistica di Fourier.

DALLA FATTORIZZAZIONE ALLA DETERMINAZIONE DEL PERIODO

Il primo trucco di questo tentativo è stato scoprire che, se si vuole fattorizzare N, si può partire dal fatto che:

è una funzione periodica ("mod" é l'operazione modulo), dove x mutualmente coprimo con N e a ≥ 0.

Poiché f (a) è periodico, ne consegue che esiste un periodo r:

poiché x^0 = 1, e considerando la natura periodica di f, che cresce da a = 0 a a = r.

A questo punto, ci si concentra su come la scoperta di r può essere raggiunta in modo quantistico per poi tornare su questa formulazione una volta noto il periodo.

TRASFORMATA QUANTISTICA DI FOURIER

Il segreto dietro l'accelerazione esponenziale si trova in questa fase dell'algoritmo: la trasformata quantistica di Fourier. Questa è un'operazione analoga a quella della trasformata discreta di Fourier. A differenza della versione classica, la trasformata quantistica di Fourier può essere implementata su porte O (n^2) (polinomiali), mentre la versione classica richiederebbe> O (2^n) (esponenziali).

La trasformata quantistica di Fourier può essere costruita utilizzando solo porte di Hadamard (H) e sfasamento (Rφ). Per ora basti dire che raggiunge il compito di scoprire r in modo esponenzialmente più velocemente rispetto ai sistemi classici, facendo uso della sovrapposizione quantistica per testare più valori contemporaneamente.

Va notato che la matematica sottostante è avanzata e, a causa del suo livello di specificità, non ha senso includerla nel testo. Tuttavia é importante comprendere il meccanismo di alto livello dietro l'algoritmo, lasciando al tempo l'eventuale curiosità e bisogno di studiarlo a fondo.

DAL PERIODO AI FATTORI

Dopo aver trovato r, ora dobbiamo tornare alla nostra aritmetica modulare ed eseguire la seguente manipolazione:

Da notare che il seguente è un multiplo di N:

Finché almeno uno di questi fattori non è un multiplo di N, ha un divisore comune con N. Quindi, va solo calcolare il massimo comune divisore (mcd) tra N e ciascuno dei 2 sopra:

Il massimo comune divisore può essere calcolato in tempo polinomiale utilizzando un algoritmo descritto più di 2300 anni fa da Euclide: l'algoritmo euclideo.

CONSIDERAZIONI SULL'ALGORITMO DI SHOR

La potenza dell'algoritmo di Shor è ancora limitata dai computer quantistici odierni (che possono avere da 50 a 70 qubit di buona qualità) e può essere utilizzata solo per fattorizzare numeri molto piccoli (che si possono fattorizzare anche manualmente).

Per rendere l'algoritmo di Shor una minaccia alla sicurezza nel mondo di oggi, occorrerebbero almeno un paio di migliaia di qubit di buona qualità, che sono comunque ancora a pochi anni di distanza.

Ci sono tempo e idee, come quella della crittografia quantistica (l'equivalente quantistico della crittografia tipica) che farà ilm sul ingresso per impedire che accadano molte catastrofi.